Global quantitative robustness of regression feed-forward neural networks

Neural networks are an indispensable model class for many complex learning tasks. Despite the popularity and importance of neural networks and many different established techniques from literature for stabilization and robustification of the training, the classical concepts from robust statistics have rarely been considered so far in the context of neural networks. Therefore, we adapt the notion of the regression breakdown point to regression neural networks and compute the breakdown point for different feed-forward network configurations and contamination settings. In an extensive simulation study, we compare the performance, measured by the out-of-sample loss, by a proxy of the breakdown rate and by the training steps, of non-robust and robust regression feed-forward neural networks in a plethora of different configurations. The results indeed motivate to use robust loss functions for neural network training.

Knowledge Augmented Machine Learning with Applications in Autonomous Driving: A Survey

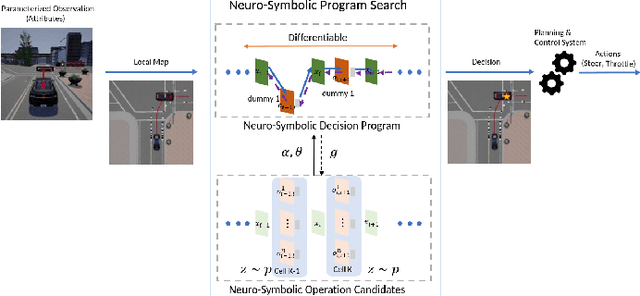
The existence of representative datasets is a prerequisite of many successful artificial intelligence and machine learning models. However, the subsequent application of these models often involves scenarios that are inadequately represented in the data used for training. The reasons for this are manifold and range from time and cost constraints to ethical considerations. As a consequence, the reliable use of these models, especially in safety-critical applications, is a huge challenge. Leveraging additional, already existing sources of knowledge is key to overcome the limitations of purely data-driven approaches, and eventually to increase the generalization capability of these models. Furthermore, predictions that conform with knowledge are crucial for making trustworthy and safe decisions even in underrepresented scenarios. This work provides an overview of existing techniques and methods in the literature that combine data-based models with existing knowledge. The identified approaches are structured according to the categories integration, extraction and conformity. Special attention is given to applications in the field of autonomous driving.

Loss-guided Stability Selection

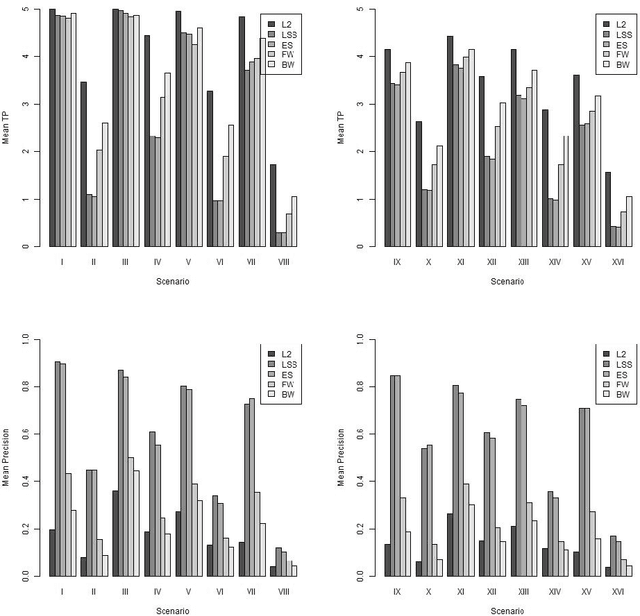
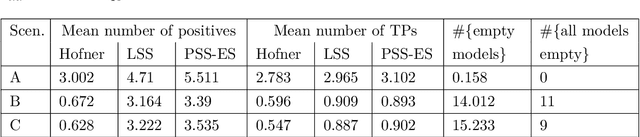
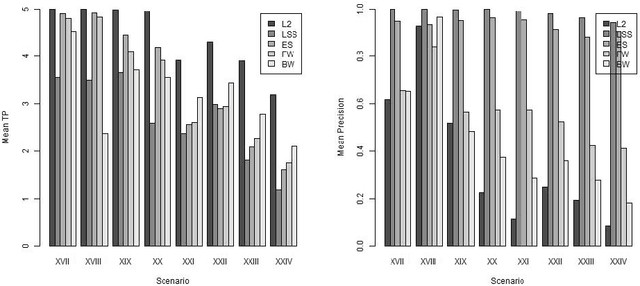
In modern data analysis, sparse model selection becomes inevitable once the number of predictors variables is very high. It is well-known that model selection procedures like the Lasso or Boosting tend to overfit on real data. The celebrated Stability Selection overcomes these weaknesses by aggregating models, based on subsamples of the training data, followed by choosing a stable predictor set which is usually much sparser than the predictor sets from the raw models. The standard Stability Selection is based on a global criterion, namely the per-family error rate, while additionally requiring expert knowledge to suitably configure the hyperparameters. Since model selection depends on the loss function, i.e., predictor sets selected w.r.t. some particular loss function differ from those selected w.r.t. some other loss function, we propose a Stability Selection variant which respects the chosen loss function via an additional validation step based on out-of-sample validation data, optionally enhanced with an exhaustive search strategy. Our Stability Selection variants are widely applicable and user-friendly. Moreover, our Stability Selection variants can avoid the issue of severe underfitting which affects the original Stability Selection for noisy high-dimensional data, so our priority is not to avoid false positives at all costs but to result in a sparse stable model with which one can make predictions. Experiments where we consider both regression and binary classification and where we use Boosting as model selection algorithm reveal a significant precision improvement compared to raw Boosting models while not suffering from any of the mentioned issues of the original Stability Selection.

The column measure and Gradient-Free Gradient Boosting

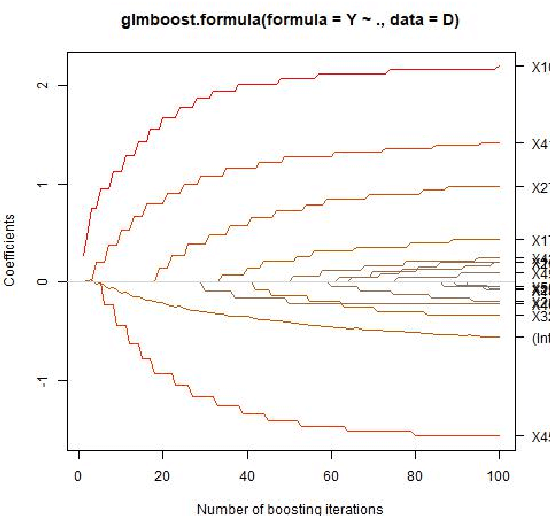
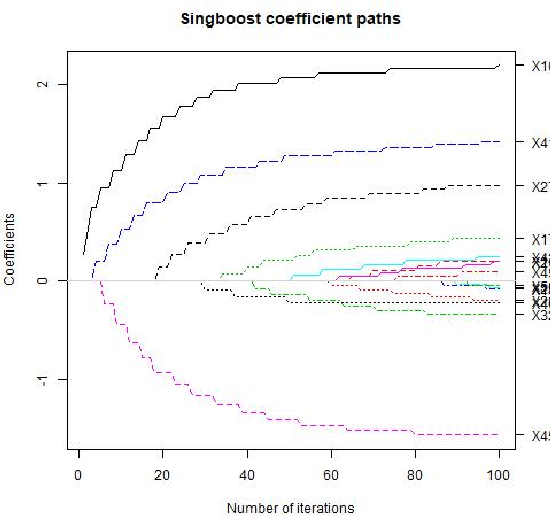
Sparse model selection by structural risk minimization leads to a set of a few predictors, ideally a subset of the true predictors. This selection clearly depends on the underlying loss function $\tilde L$. For linear regression with square loss, the particular (functional) Gradient Boosting variant $L_2-$Boosting excels for its computational efficiency even for very large predictor sets, while still providing suitable estimation consistency. For more general loss functions, functional gradients are not always easily accessible or, like in the case of continuous ranking, need not even exist. To close this gap, starting from column selection frequencies obtained from $L_2-$Boosting, we introduce a loss-dependent ''column measure'' $\nu^{(\tilde L)}$ which mathematically describes variable selection. The fact that certain variables relevant for a particular loss $\tilde L$ never get selected by $L_2-$Boosting is reflected by a respective singular part of $\nu^{(\tilde L)}$ w.r.t. $\nu^{(L_2)}$. With this concept at hand, it amounts to a suitable change of measure (accounting for singular parts) to make $L_2-$Boosting select variables according to a different loss $\tilde L$. As a consequence, this opens the bridge to applications of simulational techniques such as various resampling techniques, or rejection sampling, to achieve this change of measure in an algorithmic way.

A review on ranking problems in statistical learning

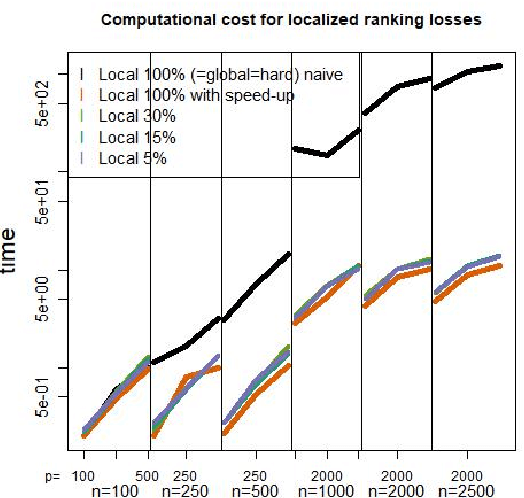
Ranking problems define a widely spread class of statistical learning problems with many applications, including fraud detection, document ranking or medicine. In this article, we systematically describe different types of ranking problems and investigate existing empirical risk minimization techniques to solve such ranking problems. Furthermore, we discuss whether a Boosting-type algorithm for continuous ranking problems is achievable by using surrogate loss functions.